数据结构 - 树的初步认识

本文讲述几种树的概念，包括二叉树、二叉查找树、AVL树和红黑树。注意本文只是对相关概念的解释，不对原理做过多的解释，特别是红黑树的添加和删除节点，是比较麻烦的情况，感兴趣者可自行研究。

一、树

树–是计算机中的一种数据结构，是一个由n（>=1）个元素组成具有层次关系的集合。因该数据结构呈现出的形状像一颗树，所以称这种数据结构叫做树，只不过这颗树是倒过来的。

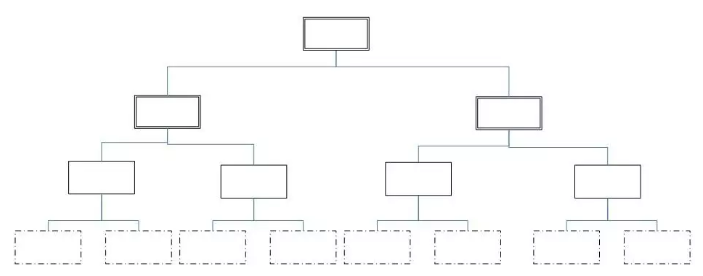
avatar

在上面的截图中，简单抽象出数据结构中的树。在生活中，这样的结构比比皆是，例如：公司的组织架构、家族的族谱、计算机中的文件结构等等。只要符合上面的结构，均可以称为树；

在计算机领域中，树只是一种简称，具体的实现还是交由其子树来完成；这其中就包括：二叉树、平衡二叉树、红黑树、B树、哈夫曼树等。

一棵树的示例图：

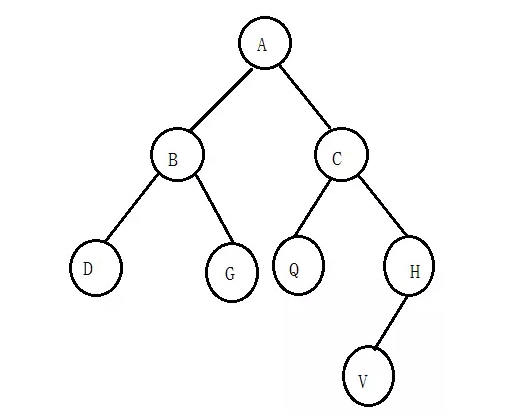
avatar

树的相关术语：

节点(Nood)：树中的每一个元素都叫做节点，又或者称为结点；图中A、B、C、D等都称之为节点；

根节点(树根-Root)：在树中，最顶端的节点称之为根节点(树根-Root)；A节点就是整个树的根节点；

子树：除了根节点之外，其余节点自由组合成的树，称之为子树，子树可以是一个节点，也可以是多个节点；其中，Q节点可称之为子树，B、D、G三个节点结合也可以称之为子树；

叶子节点(叶节点)：没有孩子节点的节点，称之为叶子节点(叶节点),也就是该节点下面没有子节点了；图中D、G、Q、V称之为叶子节点；

父节点：简单来说，就是一个节点上面的节点，就是该节点的父节点；B节点是D节点的父节点，C节点是Q节点的父节点；

树的高度：从叶子节点(此时高度为1)开始自底向上逐层增加，得到的值称之为树的高度；截图中树的高度为4（V、H、C、A）;

树的深度：从根节点(此时深度为1)开始自上而下逐层增加，最终得到的值称之为树的深度；截图中树的深度为4(A、C、H、V);

注意：关于树的高度和深度第一个节点的基数到底是0还是1，我翻过好几本数据结构的书籍各有说法，此处不做过多讨论，本文以基数为1来对待。

二、二叉树

二叉树是最基础的树结构，也是树结构中的根基。

二叉树的特点：

二叉树可以有多个元素，也可以只有一个元素，当然也可以一个元素也没有，它是一个元素的集合;

二叉树规定了在每个节点下最多只能拥有两个子节点，一左一右；其中，左节点可以称为左子树，右节点称为右子树；

二叉树没有要求左子树中任意节点的值要小于右子树中任意节点的值。

二叉树示例图：

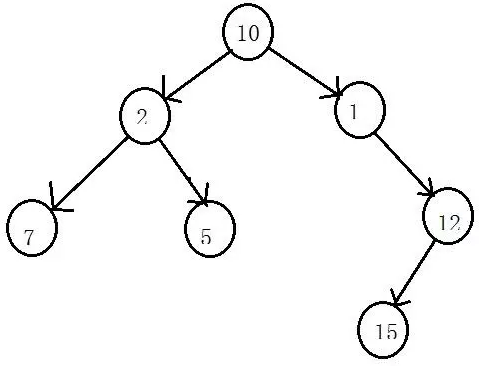
avatar

二叉树的节点实现：

public class TreeNode {
    //节点的值：
    private int data;
    //指向左孩子的指针：
    private TreeNode leftTreeNode;
    //指向右孩子的指针：
    private TreeNode rightTreeNode;
    //指向父节点的指针
    private TreeNode parentNode;

    public TreeNode(int data, TreeNode leftTreeNode,
                    TreeNode rightTreeNode, TreeNode parentNode) {
        this.data = data;
        this.leftTreeNode = leftTreeNode;
        this.rightTreeNode = rightTreeNode;
        this.parentNode = parentNode;
    }
    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public TreeNode getLeftTreeNode() {
        return leftTreeNode;
    }
    public void setLeftTreeNode(TreeNode leftTreeNode) {
        this.leftTreeNode = leftTreeNode;
    }
    public TreeNode getRightTreeNode() {
        return rightTreeNode;
    }
    public void setRightTreeNode(TreeNode rightTreeNode) {
        this.rightTreeNode = rightTreeNode;
    }
    public TreeNode getParentNode() {return parentNode;}
    public void setParentNode(TreeNode parentNode) {this.parentNode = parentNode;}
}

三、二叉查找树

二叉查找树在二叉树的基础上规定：

任一结点的值都大于其左子树，小于其右子树。

通过如上规定可以推出，二叉查找树的任意左子树和右子树中也同样形成了二叉查找树，所以说二叉查找树的特点比二叉树更加明确。

此外，根据上面的特点，我们还可以使用二分查找在树中进行元素搜索：如果查找的元素大于根节点，则在树的右边进行搜索；如果小于根节点，则在树的左边进行搜索。如果等于根节点，则直接返回；所以二叉查找树的查询效率远远高于二叉树。

二叉查找树示例图：

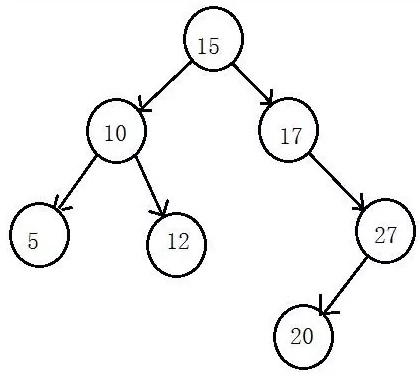
avatar

四、平衡二叉树

平衡二叉树又叫AVL树，AVL树在二叉查找树的基础上规定：

左右子树的高度差的绝对值不能大于1，也就是说左右子树的高度差只能为-1、0、1。

实际上，二叉树可以理解为一个链表结构。试想下，如果一个二叉树的左子树为空，只有右子树，且右子树中又只有右节点（左节点），那么这个二叉树就形成了一个不折不扣的链表。对于二叉查找树来说，二分查找也就失去了原有的性能，变成了顺序查找。即元素的插入顺序是1、2、3、4、5、6的话，即可实现。

AVL树示例图：

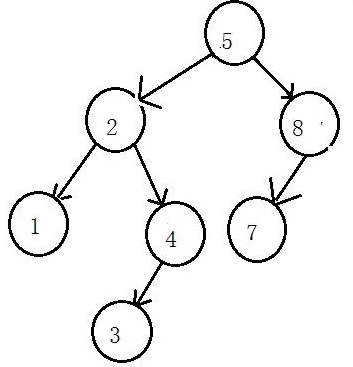
avatar

五、红黑树

1. 红黑树的定义

红黑树又叫R-B Tree，本质上是一种自平衡二叉查找树，它满足了二叉查找树的特点，即左子树任意节点的值永远小于右子树任意节点的值。红黑树和平衡二叉树(AVL树)都是二叉查找树的变体，但红黑树的统计性能要好于AVL树。因为，AVL树是严格维持平衡的，红黑树是黑平衡的。维持平衡需要额外的操作，这就加大了数据结构的时间复杂度，所以红黑树可以看作是二叉查找树和AVL树的一个折中，维持平衡的同时也不需要花太多时间维护数据结构的性质。

不过，二叉查找树还有一个致命的弱点，即左子树(右子树)可以为空，而插入的节点全部集中到了树的另一端，致使二叉查找树失去了平衡，二叉查找树搜索性能下降，从而失去了使用二分查找的意义。

为了维护树的平衡性，平衡二叉树（AVL树）出现了，它用左右子树的高度差来保持着树的平衡。而我们本节要介绍的红黑树，用的是节点的颜色来维持树的平衡。

红黑树，即红颜色和黑颜色并存的二叉树，插入的元素节点会被赋为红色或者黑色，待所有元素插入完成后就形成了一颗完整的红黑树。如下图所示：

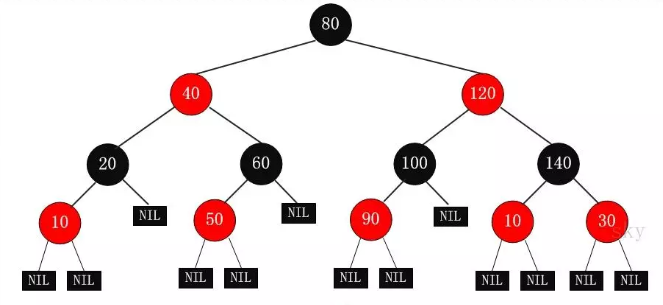
avatar

不过，你不要想当然的以为只是给二叉树的阶段随意赋为黑色或者红色，就可保证树的平衡。事情远没有你想象的那么简单。一颗红黑树必须满足以下五点要求：

树中每个节点必须是有颜色的，要么红色，要么黑色；

树中的根节点必须是黑色的；

树中的叶节点必须是黑色的，也就是树尾的NIL节点或者为null的节点；

树中任意一个节点如果是红色的，那么它的两个子节点一点是黑色的；

任意节点到叶节点（树最下面一个节点）的每一条路径所包含的黑色节点数目一定相同；

科普：NIL节点是就是一个假想的或是无实在意义的节点，所有应该指向NULL的指针，都看成指向了NIL节点。包括叶节点的子节点指针或是根节点的父指针（均是指向null的）。

红黑树的节点实现：

public class TreeNode {
    //节点的值：
    private int data;
    //节点的颜色：
    private String color;
    //指向左孩子的指针：
    private TreeNode leftTreeNode;
    //指向右孩子的指针：
    private TreeNode rightTreeNode;
    //指向父节点的指针
    private TreeNode parentNode;

    public TreeNode(int data, String color, TreeNode leftTreeNode,
                    TreeNode rightTreeNode, TreeNode parentNode) {
        this.data = data;
        this.color = color;
        this.leftTreeNode = leftTreeNode;
        this.rightTreeNode = rightTreeNode;
        this.parentNode = parentNode;
    }
    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public String getColor() {return color;}
    public void setColor(String color) {this.color = color;}
    public TreeNode getLeftTreeNode() {
        return leftTreeNode;
    }
    public void setLeftTreeNode(TreeNode leftTreeNode) {
        this.leftTreeNode = leftTreeNode;
    }
    public TreeNode getRightTreeNode() {
        return rightTreeNode;
    }
    public void setRightTreeNode(TreeNode rightTreeNode) {
        this.rightTreeNode = rightTreeNode;
    }
    public TreeNode getParentNode() {return parentNode;}
    public void setParentNode(TreeNode parentNode) {this.parentNode = parentNode;}
}

用图片来形容一个节点的话就是：

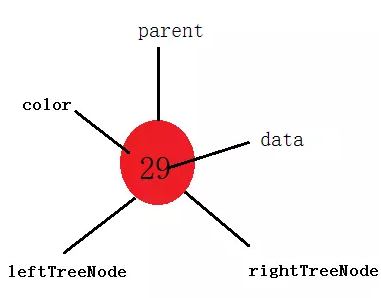
avatar

2. 红黑树的旋转

上面说过，为了维护红黑树的平衡，不只是给节点着色那么简单，还有更复杂的处理逻辑。

而这更复杂的处理逻辑就是对节点进行旋转操作，其中旋转操作又分为左旋、右旋两种；

对于树的操作，最常见的就是添加、删除而已。不过，在添加或者删除之后，红黑树发生了改变，可能就不满足以上的5点要求，也就不是一颗红黑树了。于是我们需要通过对节点的旋转，使其重新成为一颗红黑树。

A.左旋

左旋，顾名思义就是对节点进行向左旋转处理

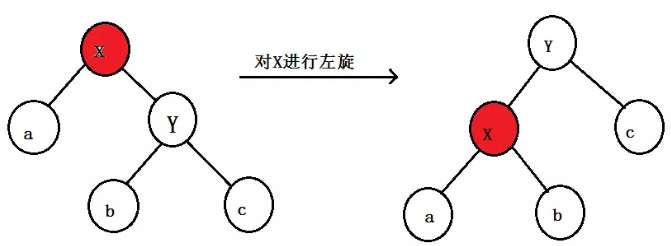
avatar

说明：

对节点X进行向左进行旋转，将其变成了一个左子节点；

这个左旋中的左，就是将被旋转的节点变成一个左节点；

其中，如果Y的的左子节点不为null，则将其赋值X的右子节点；

B.右旋

右旋，同理，也就是对节点进行向右旋转处理

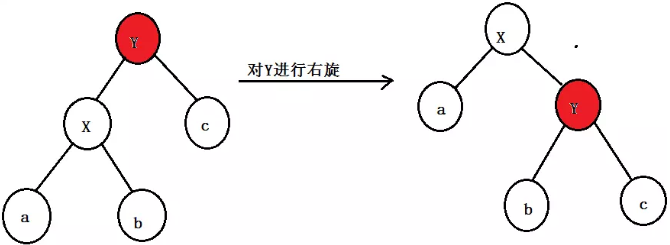
avatar

说明：

对节点Y进行向右进行旋转，将其变成了一个右子节点；

这个右旋中的右，就是将被旋转的节点变成一个右节点；

其中，如果X节点的右子节点不为null，则赋值给Y的左子节点；

3.红黑树的节点添加和删除

在将一个节点插入到红黑树中，首选需要将红黑树当做一颗二叉树查找树来对待，将节点进行插入。然后，为新插入的节点进行着色；最后，通过旋转和重新着色的方式来修正树的平衡，使其成为一颗红黑树；

对于红黑树来说，其底层依旧是一颗二叉查找树。当我们插入新的元素时，它依旧会对该元素进行排序比较，将其送入到左子树或者是右子树中。

在将新节点安置好以后，在对其进行着色处理，必须着成红色。

此时你可能会有疑问，为什么要着成红色，而不是黑色呢？

通过重新回顾红黑树必须满足的五点要求，可以分析出，当将新增节点着成红色后，我们违背以上规范的条数最少，恢复平衡起来最省事，当新增节点为红色时：

不会违背第五条 – 黑色节点数目相同；

不会违背第一条 – 节点必须是红色，或者黑色；

不会违背第二条 – 根节点是黑色。当树中已有元素时候，我们新增节点并不会影响根节点的颜色（若树中没有元素，新增节点会被当成根节点，此时虽被着为红色，但在最后一步中还会对其重新着色，变成黑色）；

不会违背第三条 – 此处所指的叶节点指的是叶节点的子节点，也就是为null的元素；

可能会违背第四条 – 任意节点为红色，其子节点一定是黑色；

然而让人更头痛的是，即便是只违背第四条，真正处理起来的时候也非常麻烦，具体的分情况处理这里不做赘述，请自行研究！